Partie B : modélisation de la stratégie de Julien par un tableur

On va maintenant s'intéresser à la somme d'argent présente sur le livret de Julien au fil des années jusqu'en 2035. Pour rappel, en 2025, Julien verse \(1~001\) €, donc l'argent présent sur le livret est de \(1~001\) €. Puis, chaque année, il verse à nouveau \(1~001\) € tandis que les intérêts de \(2{,}4~\%\) sont calculés et ajoutés à la somme présente l'année précédente.

1. Expliquer pourquoi en 2026 le montant présent, en euros, sur le livret est donné par \(1~001 + 1~001 \times 1{,}024\).
2. Calculer le montant présent sur le livret de Julien en 2027 et en 2028. Le tableur suivant résume la stratégie de Julien.

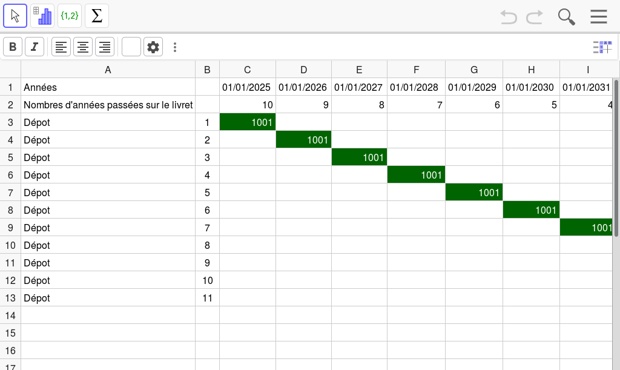
• La ligne « Nombre d'années passées sur le livret » indique le temps qu'aura passé chacun des versements de Julien sur le livret, et donc combien de fois les intérêts s'appliqueront.
  
• En vert sont indiqués tous les dépôts de \(1~001\) € réalisés depuis l'ouverture du livret.
  
• La case \(\text{D3}\) contient la somme d'argent obtenue en appliquant le taux d'intérêt de \(2{,}4~\%\) aux \(1~001\) € déposés par Julien en ouverture de livret, puisque la ligne \(3\) donne les \(1~001\) € initiaux auxquels s'ajoutent les intérêts au fur et à mesure que les années passent. Par ailleurs, cette ligne ne s'intéresse pas aux versements futurs qui sont donnés par les lignes suivantes.
  
• La colonne \(\text{M}\) contient la somme générée par chaque dépôt annuel de Julien : chaque cellule de la colonne \(\text{M}\) contient les \(1~001\) € ajoutés par Julien chaque année auxquels se sont rajoutés les intérêts. On voit donc que chaque versement aura des intérêts différents puisque ces derniers n'ont pas passé le même temps sur le livret, ce qui rend le calcul de la somme totale plus complexe que pour Ozan.
  

3. Entrer en \(\text{M3}\) la formule \(\text{=C3*1,024^10}\). Que calcule cette formule ?
On dit alors que cette valeur est la valeur acquise par le versement de \(1~001\) € placés en `2025` jusqu'à \(2035\). Compléter le reste de la ligne \(3\) en s'appuyant sur un raisonnement similaire à la cellule \(\text{M}3\).
4. On veut maintenant compléter la ligne \(4\) qui correspond aux \(1~001\) € rajoutés par Julien en 2026. Quelle formule doit-on rentrer en \(\text{E}4\) afin d'obtenir la somme d'argent correspondant ? Compléter la ligne \(4\) en poursuivant le raisonnement.
5. Compléter toute la feuille de calcul de la même manière.
6. À travers ces calculs, on vient de détailler la somme d'argent présente sur le livret. Le but est maintenant de calculer la somme totale. Quelle formule faut-il rentrer dans la case \(\text{M14}\) pour calculer la somme présente sur le livret de Julien en \(2035\) ?
7. Qui aura l'épargne la plus élevée en \(2035\) ?